Maurits Cornelis Escher es un artista particularmente conocido por sus famosos cuadros imposibles. Sus teselados, edificios irreales, escaleras interminables que suben y bajan a la vez y espacios paradójicos plasmados con meticulosos y novedosos métodos de representación, hicieron de él un personaje insólito capaz de realizar un trabajo artístico excepcional vinculado a procedimientos matemáticos.
1. Escher nació en el año 1898 Leeuwarden, capital de Frisia, una de las doce provincias del Reino de los Países Bajos. En su etapa escolar no destacó como buen estudiante. Posteriormente empezó a estudiar arquitectura en Haarlem por designio paterno pero no llegó a graduarse. Tras abandonar sus estudios se convirtió en discípulo del profesor de artes gráficas Samuel Jessurun de Mesquita, bajo cuyas enseñanzas llegó a adquirir destreza en el dibujo y en la técnica de impresión con plancha de madera llamada xilografía.

2. Dos años más tarde viajó a Italia donde se dedicó principalmente a pintar paisajes. Pasó por España y se fascinó por los diseños geométricos de la Alhambra, lo cual fomentó su interés por la división del plano y los patrones matemáticos. En Italia permaneció hasta 1935 con su esposa, sin embargo, salió del país por la situación política y se estableció en Suiza durante dos años. En ese país no se sintió cómodo, por lo que se trasladó nuevamente a Bélgica, pero la Segunda Guerra Mundial le obligó a volverse a mudar a Holanda.

3. La fama y el reconocimiento artístico le llegaron a finales de los años 50. No obstante, no fue hasta principios de esa misma década que la venta de sus obras no le proporcionaron un sustento económico para vivir independientemente. Escher logró vender copias de sus grabados y hacer diseños por encargo, lo cual le otorgó una situación dineraria óptima a través de una producción y reproducción regular de trabajos. Su actividad se vio reducida tras dificultades de salud. Finalmente, en marzo de 1972 acabó falleciendo en Hilversum.

4. Las obras más conocidas de Escher son representaciones tridimensionales que físicamente son imposibles de realizar. Sin embargo este tipo de dibujos sólo comprenden una pequeña parte del conjunto de su obra. Del mismo modo, son característicos los ciclos, las metamorfosis, las aproximaciones al infinito, los cuerpos matemáticos, los paisajes, etc. En sus dibujos destacan los detalles realizados con una exactitud minuciosa y la integración de las matemáticas en el arte. Su destreza artesanal es también remarcable: manejaba con maestría técnicas como la mencionada xilografía, la litografía (con planchas de piedra) y el grabado a media tinta.
5. Entre los años 1922 y 1935, la etapa italiana, Escher representó paisajes de modo casi exclusivo. El detallismo y el juego de luces y sombras son los rasgos que predominan. Es al final de este período cuando empieza a experimentar con el concepto de los reflejos. En 1935 realizó la litografía Mano con esfera de espejo. En esta obra refleja una precisión extraordinaria tanto en los detalles como en las formas propias de los reflejos.

6. La salida de Italia le alejó de los paisajes que tanto le motivaban, y los temas de sus obras cambiaron. En su etapa de Suiza y Bélgica (entre 1935 y 1941) se enfocó en el concepto de la división del plano. Su interés tenía una expresión artística, pero se basaba en un estudio matemático. Dicho concepto fue una verdadera obsesión durante toda su vida. Él mismo expresó que era su fuente más rica de inspiración. En 1936 visitó por segunda vez la Alhambra e intentó copiar los motivos representados en el decorado. Adoptó un sistema para configurar particiones periódicas del plano y descubrió diecisiete grupos de simetría en el edificio. De este modo, muchos de sus cuadros son teselas que cubren la integridad del plano sin espacios libres, conformando frisos y mosaicos. A partir de figuras geométricas simples creaba otros patrones con formas de animales, humanos y objetos.

7. Otro tema importante es la metamorfosis. Ésta no consiste en otra cosa más que en figuras repetidas que se van trasformando en toras distintas de forma gradual. Este concepto lo combinó frecuentemente con la partición del plano, de modo que las teselas tienen una figura en un extremo y progresivamente adopta otra forma distinta en el otro extremo.

8. El ciclo es fundamentalmente lo mismo que una metamorfosis pero que se cierra en sí mismo completando la etapa de modo igual al que comienza. De esta manera, el final del proceso y el inicio son estrictamente coincidentes. En estos diseños, los elementos visuales vuelven sobre sí mismos.

9. En su segunda etapa holandesa, entre 1941 y 1955, Escher ya había alcanzado la madurez y mezcla los elementos y los temas desarrollando, así, trabajos más complejos. La división del plano, el ciclo y la metamorfosis son trasladados a una representación tridimensional. Sus obras Reptiles y Espejo mágico son buena muestra de ello.

10. A partir de entonces empieza a florecer su interés por lo infinito y por las geometrías imposibles. Una de los primeros experimentos dentro del ámbito de las geometrías tridimensionales imposibles es su obra de 1953 Relatividad. Lo interesante de esta construcción es que la imposibilidad no radica en las tres escaleras, sino las tres fuerzas de gravedad actuando de forma diferente y a la vez. La sensación de irrealidad la hace notar con los personajes que figuran en la obra a los que les afecta la gravedad en direcciones distintas.

11. El propio Escher expresó en un artículo la importancia de la idea de infinito, la cual pretende representar en muchos de sus trabajos. La partición regular del plano no consigue plasmar el infinito completamente, de modo que exploró otras técnicas para representar el infinito artísticamente. Para dibujar infinitas figuras en un espacio finito dibujó figuras que encajaban entre ellas, de manera que iba rellenando la superficie con formas que disminuían su tamaño progresivamente. La impresión de que hay infinitas figuras la consigue mediante el método por el cual la suma del área de las mismas es una serie convergente.

12. Su última etapa transcurre entre 1955 y 1972 (el año de su muerte). En ella se enfocó en la división del plano (su tema predilecto) y en los límites. Escher descubrió el concepto de división hiperbólica a raíz de una conversación con el matemático Coxeter, uno de los grandes geómetras del siglo XX. Haciendo uso del concepto trabajó en una serie llamada Límite circular. Las leyes matemáticas de la Introducción a la geometría de Coxeter permitieron a Escher aproximarse desde una nueva perspectiva al concepto de infinito (se fijó particularmente en un mosaico hiperbólico de Poincaré). Los grabados de esta serie tienen líneas curvas que enfatizan la sensación de volumen, por lo que da la impresión de observar una esfera.

13. La litografía titulada Cóncavo y convexo de 1955 es una de las más representativas del artista. En ella se puede observar una construcción recorrida por varias escaleras cuyos elementos mantienen una ambigüedad geométrica y juega con la perspectiva. A este respecto, las columnas son las que más destacan, ya que pueden verse o interpretarse como cóncavas o convexas según el criterio del espectador. La definición de la convexidad o concavidad depende de los elementos de referencia con los que Escher juega, dado que también son ambiguos.

14. En su obra de 1958 Belvedere encontramos un edificio de tres plantas con elementos incongruentes armonizados en la representación artística. Los pisos del edificio parece que tienen orientaciones distintas.

15. Subiendo y bajando es una litografía de 1960. Se trata de una curiosa paradoja visual que presenta una escalera sin fin en lo alto de un edificio. Es un recorrido cuadrado aparentemente cerrado cuyos escalones siempre suben o siempre bajan según el sentido de la circulación. El efecto queda acentuado con los personajes que transitan la escalera. El efecto de la escalera sin fin lo consigue mediante la perspectiva en la que se observa el recorrido, puesto que en realidad la planta de la torre no está cerrada. Desde el particular punto de vista del dibujo parece que el primer y el último escalón coinciden en altura.


16. En la litografía de 1961 La cascada se observa una construcción con un molino de agua sobre un paisaje escalonado. Es un dibujo que supone una paradoja, ya que el circuito que recorre el agua es horizontal en apariencia pero al final del mismo hay un fascinante efecto óptico de caída del agua valiéndose del triángulo de Penrose en la estructura arquitectónica de la que cae la cascada.

17. Escher se interesó por los objetos imposibles y ambiguos como el cubo de Necker que aparece en Belvedere. La figura imposible que más destaca es el denominado triángulo de Penrose. Se trata de un aparente triángulo tridimensional que no se puede construir en la realidad. Aparenta ser un sólido construido por tres segmentos rectos cuya sección es cuadrada, cuya unión forma ángulos rectos. Tales propiedades no pueden darse a la vez en un cuerpo tridimensional en un espacio euclídeo. Esta figura, también llamada “tribar” fue creada por Oscar Reutersvärd y redescubierta por Roger Penrose años después.

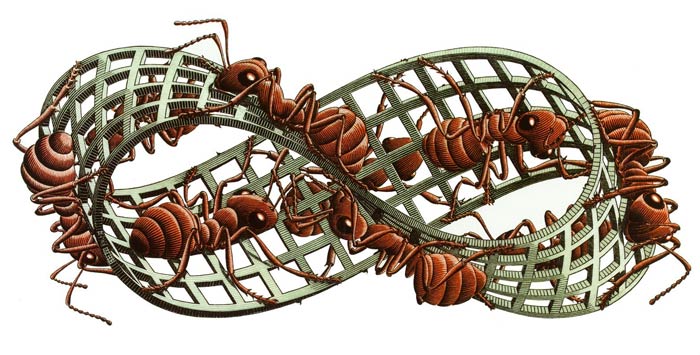
18. La cinta de Möbius es una superficie reglada con una única cara y un único borde. Escher experimentó con esta idea en Jinetes antes de tener un conocimiento explícito de esta estructura topológica. Esta forma permite representar un efecto de movimiento perpetuo sin un comienzo determinado ni fin.
19. La idea de transformación continua es abordada en el trabajo de Escher particularmente en sus diseños espirales. El tamaño de las figuras va creciendo y disminuyendo siguiendo un recorrido. Tanto la trayectoria como el desarrollo de los tamaños generan un efecto visual de fondo sin fin.

20. En 1969 Escher demuestra que, a pesar de la avanzada edad y la debilidad de salud, sigue manejando las técnicas con maestría y conservando su creatividad. De esa fecha es su obra Serpientes, la cual es la máxima expresión de las representaciones de límite circular entretejiendo una urdimbre que se intercala con las figuras de tres serpientes.

Bibliografía
Acevedo Quero, F. (2007). Escher y el arte imposible. Manual formativo de ACTA. N. 45, pp. 61-74.
Rojo, M. (2009). Escher y las matemáticas. Revista argentina de psicopedagogía. N. 62.