Dicen que la banca siempre gana, aunque en realidad los juegos de azar no son más que una combinación conjunta de matemáticas, estadística y probabilidad.
Los números gobiernan el universo, los dados y los tapetes verdes de las mesas de los casinos. Quien domina los números, también puede llegar a dominar todo lo anterior.
El famoso problema de Monty Hall es un desafío de probabilidad inspirado en el conocido concurso televisivo estadounidense Let’s Make a Deal («Hagamos un trato»), emitido entre los años 1963 y 1986.

Recibe su nombre directamente del presentador del programa, el popular actor Monty Hall:
En este concurso, el participante debe escoger una puerta entre tres, y su premio será aquello que se encuentra detrás de la puerta elegida.
Una de ellas oculta un coche de alta gama, y tras las otras dos hay una cabra.
El participante escoge la puerta número 2, la del centro. A continuación, el presentador, que sabe dónde se encuentra cada premio, se adelanta y abre la puerta número 1, revelando que detrás de ella había una cabra.
Ahora le ofrece al concursante una oportunidad de cambiar la puerta escogida, sabiendo que la puerta número 1 ocultaba una cabra.
Ahora quedan un coche y otra cabra.
¿Debería el concursante mantener su elección original para obtener el coche o cambiar de puerta? ¿Es indiferente o tiene más probabilidades de conseguir el vehículo si decide probar suerte con la puerta número 3?

A simple vista, parece que debería darle igual cambiar o no de puerta.
Todo parece indicar que, eliminada la opción de la puerta número 1, la posibilidad de obtener el coche queda determinada en un 50% de probabilidades entre las puertas 2 y 3.
Pero si fuera tan fácil, no existiría este problema ni se hubiera hecho tan famoso, ¿no crees?
En realidad, el concursante obtendría mayor probabilidad de conseguir el ansiado coche si cambia de puerta una vez revelada la ubicación de una de las cabras.
Es decir, que si estuvieras jugando con las puertas que aparecen arriba y bajo las condiciones anteriormente descritas, deberías abrir finalmente la puerta verde para asegurarte más opciones de llevarte el coche a casa.
¿Por qué ocurre esto?
Este problema ha generado siempre mucha polémica a lo largo de su existencia. Su solución ha sido permanentemente discutida en libros y periódicos hasta la llegada de Internet, promulgándose la primera respuesta matemáticamente fundada en un artículo de Marilyn vos Savant en la revista estadounidense Parade durante el año 1990. Su publicación generó una auténtica avalancha de críticas que duran hasta el día de hoy.
Vamos a intentar resolver el problema paso a paso.

Si el jugador escoge inicialmente la puerta número 1 (la roja, con una cabra), y finalmente se la queda, se llevaría el animal a casa. Pero si la cambiara, obtendría el coche.
Si el jugador escoge inicialmente la puerta número 2 (la amarilla, con una cabra), y finalmente se la queda, le tocaría llevarse a la cabra. Si cambiara, conseguiría el coche.
Si el jugador escoge inicialmente la puerta número 3 (la verde, con un coche), y se la queda, tendría suerte y se llevaría el coche a casa. Si cambiara, ganaría una cabra.
Como podemos comprobar, solo en una tercera parte de los casos el concursante ganaría un coche sin cambiar de puerta después de elegir una (si escogiera la puerta número 3).
Sin embargo, cambiando de puerta se aseguraría la obtención del coche en dos terceras partes de los casos (habiendo escogido previamente las puertas número 1 ó 2).
¿Qué te parece más probable: elegir una de las puertas 1 y 2 o escoger la puerta 3?
Dos de las puertas aseguran la obtención de un coche cambiando de elección después de que el presentador descubra una de las cabras, mientras que solo una ellas lo asegura manteniéndote firme en tu elección original.
Puede que el siguiente esquema te ayude a comprenderlo mejor.
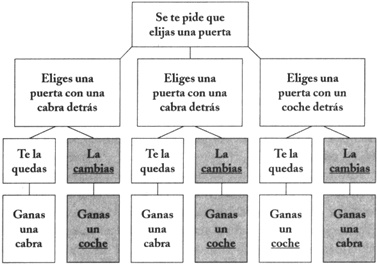
Curioso, ¿verdad?
Ahora ya sabes cómo ganar un coche completamente gratis.