A lo largo de una década dedicada al urbanismo muchas veces escuché llamar mentirosos a los mapas. Los paisanos siempre querían llevarme al terreno para comprobar lindes o medir distancias. Había dinerales en juego y no se fiaban de los interminables rollos de cartografía catastral que siempre viajaban conmigo. «Los mapas mienten» me decían. Y no les faltaba razón.
Aquellos eran planos de gran escala, entre 1:1 000 y 1:10 000 normalmente, los habituales cuando se elaboran documentos de planeamiento urbanístico. Con ese grado de detalle la cartografía representa porciones del terreno lo bastante reducidas como para que la curvatura terrestre no sea relevante. Sin embargo el relieve sí que lo es, o al menos puede llegar a serlo, porque topográficamente hablando no es lo mismo trabajar sobre una llanura, donde todo es mucho más sencillo, que enfrentarse a una zona de montaña, donde las distancias reducidas u horizontales dejan de darse la mano con las distancias reales o topográficas. En estas últimas, en las áreas montañosas, la tan indeseable tercera dimensión se manifiesta con mayor fuerza -indeseable cuando lo que se pretende es plasmar la realidad en un papel-.
Esa dimensión extra es el enemigo de la cartografía, algo que conocen muy bien quienes se dedican a elaborar mapas de nuestro planeta. En este caso el relieve de la superficie terrestre pasa a ser algo anecdótico -a la escala de un mapamundi sería absurdo preocuparse por él-, el desafío reside aquí en proyectar con el mayor grado de precisión posible un cuerpo aproximadamente esférico, es decir, de tres dimensiones, sobre un plano. Porque, por más que prediquen lo contrario hordas de pseudocientíficos, para desgracia de los cartógrafos la Tierra se parece más a un balón de fútbol que a una pizza. Lo que sigue a continuación tiene que ver con algunas de las dificultades inherentes a la proyección de un cuerpo tridimensional sobre una superficie bidimensional. Terraplanistas abstenerse.
Trasladar la realidad terrestre a un planisferio exige necesariamente ciertas renuncias. Entrar en detalle sobre los porqués del asunto espesaría bastante este artículo y no es esa mi intención, así que simplemente vamos a quedarnos con que no existe el mapa perfecto. Y no existe porque hacerlo es matemáticamente imposible. Algunas de las proyecciones cartográficas empleadas se centran en representar con fidelidad las distancias relativas, otras la proporcionalidad de las áreas y, finalmente, están las orientadas a conservar los ángulos. Sin embargo, esas tres propiedades, es decir, equidistancia, equivalencia y conformidad, no pueden aunarse bajo una única proyección.
En el siglo XVI el cartógrafo flamenco Gerardus Mercator abordó el desafío de manera tan eficaz que su legado ha conseguido llegar hasta la actualidad: se puede encontrar desde en los clásicos atlas escolares hasta en servidores de mapas online, como el todopoderoso Google Maps. La temprana aceptación de la proyección de Mercator tuvo que ver con lo apropiada que resultaba para elaborar cartas náuticas en una época en la que los navegantes comenzaban a descubrir el mundo. En nuestro tiempo las plataformas de cartografía web justifican su empleo por lo conveniente de la disposición de paralelos y meridianos, siempre horizontales y verticales, respectivamente, y por su carácter conforme, es decir, respetuoso con los ángulos. Han sido cinco siglos de éxito incontestable.
El precio a pagar por tantas virtudes fue el sacrificio de la fidelidad a distancias y áreas. Y por ello ha sido duramente criticada, especialmente en los últimos tiempos. Algunos han querido ver en la proyección de Mercator una visión eurocéntrica del mundo, la plasmación de la preeminencia del Norte sobre el Sur hecha mapa. Y bueno, respecto a esta cuestión existen opiniones para todos los gustos, pero si queréis conocer la mía os diré que más que intencionalidad política yo veo los problemas cartográficos inherentes al empleo de una proyección cilíndrica. Un tipo de proyección que resulta absolutamente fiel en el ecuador, es decir, en la línea en la que el globo terrestre es tangente al cilindro de desarrollo que la contiene, y que sin embargo empieza a acumular distorsiones a medida que la latitud se incrementa hasta llegar a la total aberración en las cercanías de los polos geográficos, convirtiendo, por ejemplo, a Groenlandia en descomunal sobre el papel, tan grande como África, cuando en realidad es muchísimo más pequeña.
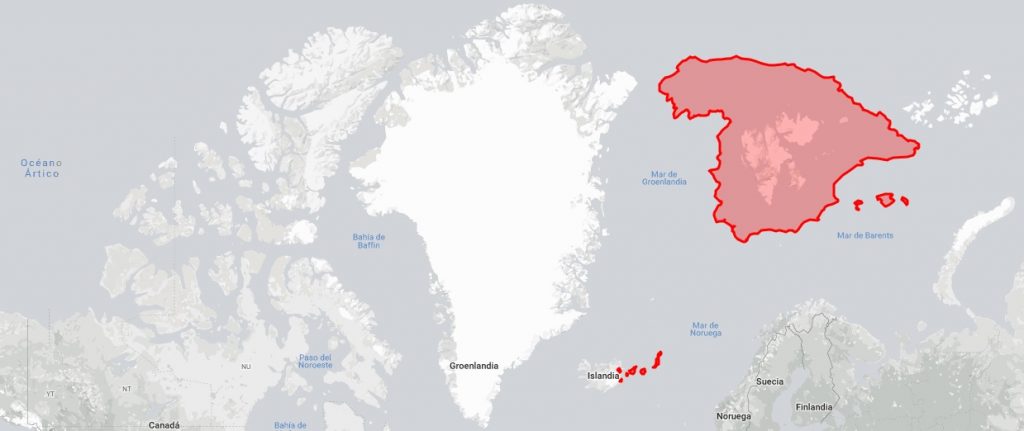
Todas las capturas de pantalla que ilustran esta entrada proceden de thetruesize.com, una web que permite tomar conciencia de las desviaciones en la representación de los distintos países en función de su ubicación geográfica. Yo, para entretenerme un rato, he agigantado a España situándola sobre el archipiélago Svalbard, y he empequeñecido a Groenlandia al colocarla frente a las costas de Portugal, a una latitud muy inferior a la que ocupa. Trastead un poco en esa página de internet y enseguida veréis hasta qué punto se aleja de la realidad el clásico mapamundi, ese que habita en el subconsciente colectivo.
Ante la imposibilidad de conseguir la proyección perfecta -ya decíamos que tal perfección no puede existir-, una alternativa es optar por una solución de compromiso que renuncie a la exactitud en un parámetro determinado a cambio de la reducción de los distorsiones en todos ellos: es el caso de las denominadas proyecciones modificadas. Entre ellas se encuentra la de Winkel-Tripel, adoptada por instituciones como la National Geographic Society para sus mapas.
En todo caso, si queréis tener una idea verdaderamente cabal de cómo es en realidad el planeta que habitamos, os aconsejo echar un vistazo a un globo terráqueo. No hemos inventado nada mejor.